各种想法都有自己的一席之地,但是时间会剔除许多细节。
$P=(x_0,y_0)$ 是抛物线$y=x_2$上的任意一个定点,如图2.4所示。作为基本思想的第一个图例,给定抛物线上一点P,计算切线的斜率。首先,我们选择曲线上的一个临近点 $Q=(x_1,y_1)$。接下来,我们画出由这两点确定的割线$PQ$,割线的斜率明显是:
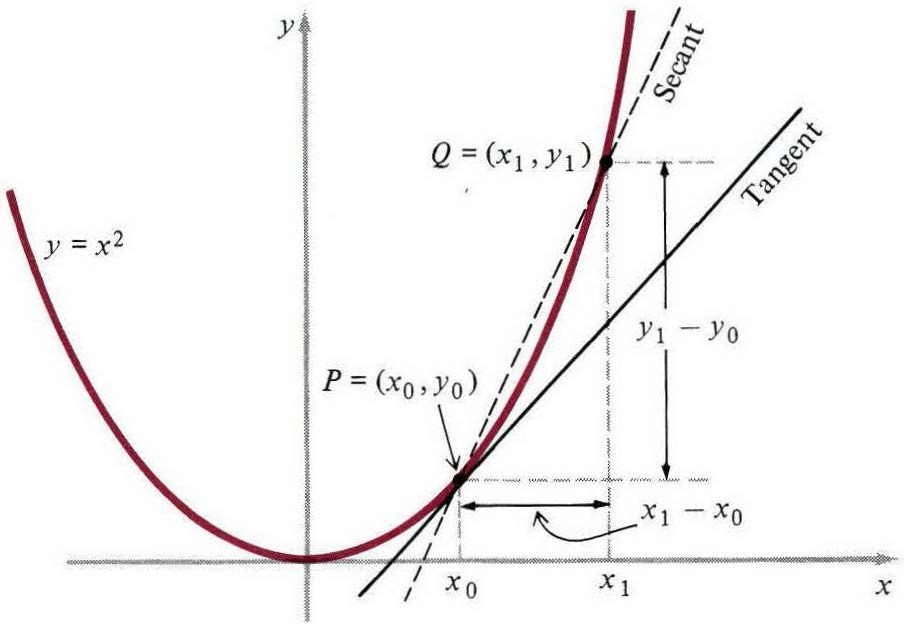
图一
现在是关键的一步︰我们让 $x_1$ 靠近 $x_0$,以便点$Q$接近定点$P$,就像一串沿着线滑动的佛珠。这样的话,割线开始改变方向并明显接近 $P$。而且,直观上来看,切线的斜率是割线斜率计算得到的极限值。用标准符号来表达就是:
缩略词“lim”且下方有“$x_1\to x_0$”读作“当$x_1$趋向$x_0$,…的极限是”。
我们不能简单的设置 $x_1=x_0$ 来计算极限值$m$,因为那样的话$y_1=y_0$并且给出了无意义的结果:
我们必须将 $x_1$ 看做非常接近 $x_0$ 而有别于它。然而,当 $x_1$ 趋进 $x_0$ 时,$y_1−y_0$和$x_1−x_0$变的非常小,他们商的极限值是多少并不清楚。
解决这个困难的办法是用曲线的方程。因为$P$和$Q$都落在曲线上,我们有$y_0=x_0^2$和$y1=x_1^2$,所以(1)可以写成:
分子变小的原因是它的一个因子包含分母。如果约掉这个公因子,得到:
(2)式就变成:
现在明显的看到:当$x_1$越来越接近$x_0$时,$x_1+x_0$越来越接近于等式$x_1+x_0=2x_0$。相应的:
是曲线$y=x^2$在点$P(x_0,y_0)$处切线的斜率。
例1:点(1,1)和(-1/2,1/4)在抛物线$y=x^2$(图2)上。根据(4),这些点切线的斜率是$m=2$,$m=−1$。用直线的点斜方程,两条切线明显有两个方程:
同样的,
是点$(x_0,x_0^2)$处的切线方程。
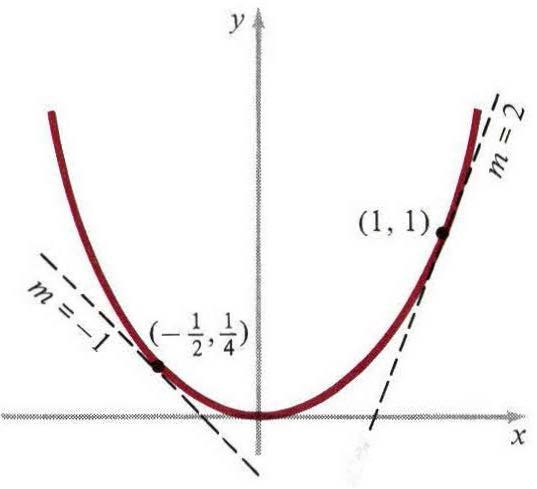
图二
现在我们介绍一个被广泛使用的符号,读作delta。
刚刚描述的过程从独立变量$x$的变化量开始。这种变化量的标准符号是$\Delta x$,所以
是x从第一个值到第二个值的变化量。我们也可以将第二个值看成是第一个值加上变化量得到的:
$x$ 不是一个数$\Delta$和一个数$x$的乘积,而是一个数,叫做$x$的增量。增量$x$可以为正也可以为负。因此,如果$x_0=1$,$x_1=3$,那么$x=3−1=2$;如果$x_0=1$,$x_1=−2$,那么$x=−2−1=−3$。
字母$\Delta$是希腊字母$d$;当它写在一个变量前面时,它表示该变量两个值之差。这个简单的符号是极为方便的,几乎扩展到数学和科学的每个部分。我们用它来重写上述计算过程。
将(5)或(6)带入(3)的:
这一次没有分解分子,我们增加了它的第一项,化简得:
所以(7)变为:
如果我们将它带入(2),利用$x1\to x0$等价于$\Delta x\to 0$,我们发现:
跟之前的结果一样。再次看到指定的极限过程发生了什么:随着$x$越来越趋近于0,$2x_0+\Delta x$越来越趋近于$2x_0$。
第二种方法(即使用delta符号)取决于扩大$(x_0+x)^2$,而第一种取决于分解表达式$x_1^2−x_0^2$。这种特定情况下,两种计算明显比其他方法容易。然而,第二种比第一种容易,为此我们采用增量作为我们的标准过程。
我们只进行了抛物线$y=x^2$的计算,理论上,任何函数$y=f(x)$(图3)都可以用此计算进行描述。我们首先计算通过两个点$P$和$Q$(对应于$x_0$和$x_0+x$)割线的斜率:
然后计算$x$趋进$0$时$m_{sec}$的极限,得到一个数$m$,几何上它是曲线上点$P$割线的斜率:
这个极限值经常用$f’(x_0)$表示,来强调它依赖于点$x_0$和函数$f(x)$。因此,根据定义我们有:
上面给出的计算结果也可以表示为:如果$f(x)=x_2$,则$f′(x_0)=2x_0$。
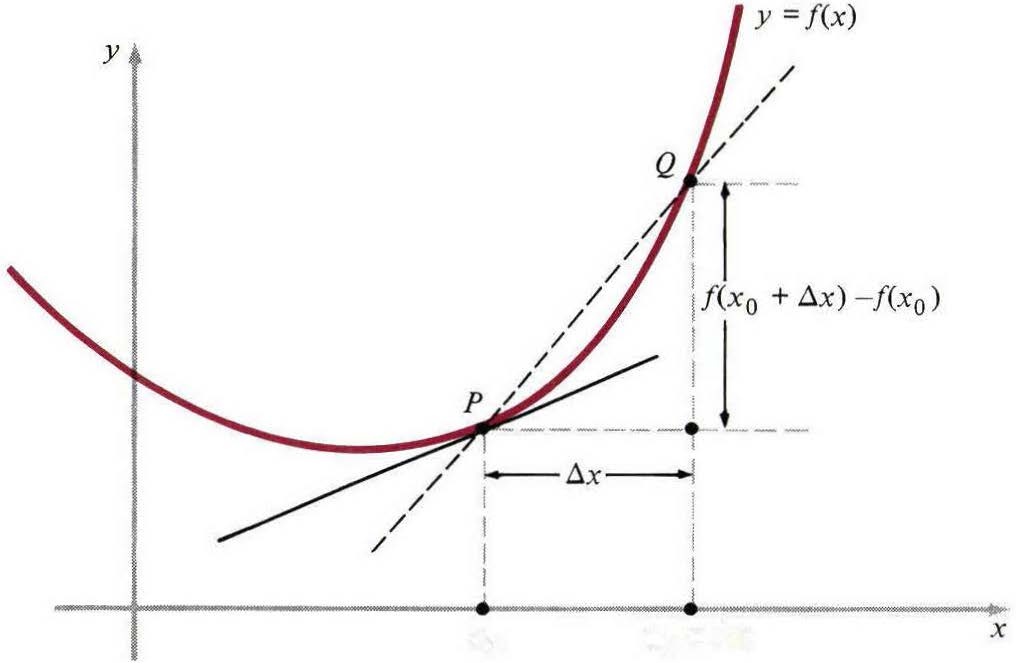
图三
例2:计算$f′(x0)$ 其中$f(x)=2x_2−3x$
解:(8)中的分子是:
因此(8)变为:
我们根据假设得到 (8),即曲线有单一明确的切线。这的确是个假设,因为一些曲线并没有这种切线(图4)。然而,当切线存在时,它显然需要割线$PQ$靠近极限位置,无论$Q$是从右还是从左。这两种方法区别在于$x$靠近$0$时是只通过正值还是只通过负值。当极限存在时,两个方向靠近得到的极限值相同,这是(8)含义的一部分。
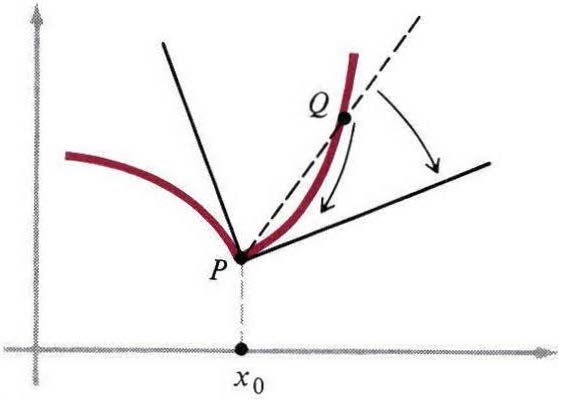
图四