漫步微积分2.3 - 导数的定义

从几何上考虑，我们利用2.2，并丢掉下标$x_0$，就得到导数的基本定义：给定任意函数$f(x)$，导数$f′(x)$是新的函数，在点$x$处的值定义为

$$\begin{equation} f'(x)=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\tag1 \end{equation}$$

在计算它的极限时，$x$是固定的，而$\Delta x$是变化的且接近于零。某些$x$存在极限值，某些却不存在。如果$x=a$的极限值存在，就说函数在点$a$处可导。如果一个函数在其定义域内的每个点均可导，那么该函数是可导函数。这本书讨论的大部分函数都有此性质。
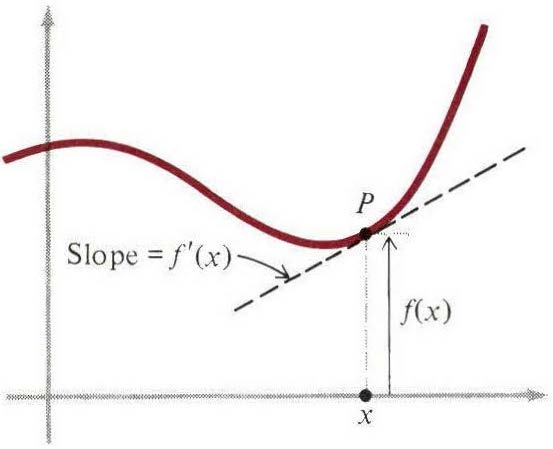
我们知道$f′(x)$可以像图1那样可视化，在图中$f(x)$是曲线上动点$P$的高度。然而，严格意义上讲，上述的导数定义不依赖于任何几何想法。图1构成一种几何解释，对理解导数来说非常重要，可以作为一种辅助手段，但它不是导数概念的基本组成部分。下一节我们将看到其他与几何无关的解释，那些解释跟几何解释同等重要。因此，我们必须将$f′(x)$作为纯粹的函数，并且需要认识到它有多种解释，但与其中任何之一都没有必要的联系。

实际上形成导数$f′(x)$的过程称为给定函数$f(x)$的微分。这是微积分的基本运算，其他一切依赖于此。原则上，我们遵循（1）中指定的计算说明。这些说明可以整理为一个系统的过程，叫做三步法。
第一步：写出函数的差$f(x+\Delta x)−f(x)$。
第二步：除以$\Delta x$得到差商的形式

$$\frac{f(x+\Delta x)-f(x)}{\Delta x}$$

大部分问题只涉及分子分母消去$\Delta x$
第三步：估计$\Delta x\to 0$时的极限值。如果第二步已经完成了，那么该步可以作为简单的检查。
如果我们记得符号$f(x)$几乎包含了所有可以想象到的函数，那么我们将了解到这些步骤有时容易，有时很难。下面的示例只涉及初等代数，但即使如此，还是需要一点知识和技巧。

例1:对函数$f(x)=x^3$求$f′(x)$
第一步：

$$\begin{eqnarray*} f(x+\Delta x)-f(x) &=&(x+\Delta x)^3-x^3\\ &=&x^3+3x^2\Delta x+3x\Delta x^2+\Delta x^3-x^3\\ &=&3x^2\Delta x+3x\Delta x^2+\Delta x^3\\ &=&\Delta x(3x+3x\Delta x+\Delta x^2) \end{eqnarray*}$$

第二步：

$$\frac{f(x+\Delta x)-f(x)}{\Delta x}=3x+3x\Delta x+\Delta x^2$$

第三步：

$$f'(x)=\lim_{\Delta x\to 0}[3x+3x\Delta x+\Delta x^2]=3x^2$$

例2:对函数$f(x)=1/x$求$f′(x)$
第一步：

$$\begin{eqnarray*} f(x+\Delta x)-f(x) &=&\frac{1}{(x+\Delta x)}-\frac{1}{x}\\ &=&\frac{x-(x+\Delta x)}{x(x+\Delta x)}=\frac{-\Delta x}{x(x+\Delta x)}\\ \end{eqnarray*}$$

第二步：

$$\frac{f(x+\Delta x)-f(x)}{\Delta x}=-\frac{1}{x(x+\Delta x)}$$

第三步：

$$f'(x)=\lim_{\Delta x\to 0}\frac{1}{x(x+\Delta x)}=-\frac{1}{x^2}$$

让我们简要地分析一下例2的结果告诉了我们哪些关于函数$y=f(x)=1/x$图像的信息。首先，多所有$x\neq 0\ f’(x)=-1/x^2$为负值，而且由于这是切线的斜率，所有切线斜向右下方。更进一步，当$x$接近0时，$f′(x)$非常大，这意味着切线非常陡峭的;而当$x$很大时，$f′(x)$非常小，所以切线是趋近水平的。通过测试图来验证我们的观察时很有启发意义的。一般来说，导数能够告诉我们许多函数的行为以及图像的性质，因为某点的导数给出的了该点的切线斜率。我们之后会更加充分的探讨这一主题。
例3:对函数$f(x)=\sqrt{x}$求$f′(x)$
第一步：

$$f(x+\Delta x)-f(x)=\sqrt{(x+\Delta x)}-\sqrt{x}\\$$

第二步：

$$\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{\sqrt{(x+\Delta x)}-\sqrt{x}}{\Delta x}$$

这种形式不方便取消$\Delta x$，所以我们用一个巧妙的代数技巧去除分子中的平方根。分子和分母均乘以$\sqrt{x+\Delta x}+\sqrt{x}$，这就相当于分数乘以1，然后我们使用代数式$(a-b)(a+b)=a^2-b^2$进行简化：

$$\begin{eqnarray*} \frac{f(x+\Delta x)-f(x)}{\Delta x} &=&\frac{\sqrt{x+\Delta x}-\sqrt{x}}{\Delta x}\cdot \frac{\sqrt{x+\Delta x}+\sqrt{x}}{\sqrt{x+\Delta x}+\sqrt{x}}\\ &=&\frac{(x+\Delta x)-x}{\Delta x(\sqrt{x+\Delta x}+\sqrt{x})}\\ &=&\frac{1}{\sqrt{x+\Delta x}+\sqrt{x}} \end{eqnarray*}$$

现在第三步就容易了。
第三步：

$$f'(x)=\lim_{\Delta x\to 0}\frac{1}{\sqrt{x+\Delta x}+\sqrt{x}}=\frac{1}{\sqrt{x}+\sqrt{x}}=\frac{1}{2\sqrt{x}}$$

符号的一些说明

微积分有个令人困惑的特点，就是几个不同的符号都可以用来表示微分，符号的使用带有某种偏好，通过环境来选择相应的符号。可能有人会问，使用这些符号有什么问题吗？事实是，问题很大，好的符号可以铺平道路，为我们做许多工作，而不好的类似于沼泽，很难轻松移动。

函数$f(x)$的导数上文表示为$f′(x)$。这个符号的优点在于强调$f(x)$的导数是关于x的另一个函数，它与给定函数以某种方式关联起来。如果我们给出的函数形式为$y=f(x)$，即用一个独立变量来表示，那么更短的符号$y′$常用来代替$f′(x)$。

用这种符号来表示导数最大的缺点是它没有显示出$f(x)$得到$f′(x)$过程。从这个层面考虑莱布尼兹设计的符号更好，当然在其他方面也不错。

下面解释莱布尼兹的符号，对一个函数$y=f(x)$，它的差商形式

$$c{f(x+\Delta x)-f(x)}{\Delta x}$$

可以记为

$$\frac{f(x+\Delta x)-f(x)}{\Delta x}$$

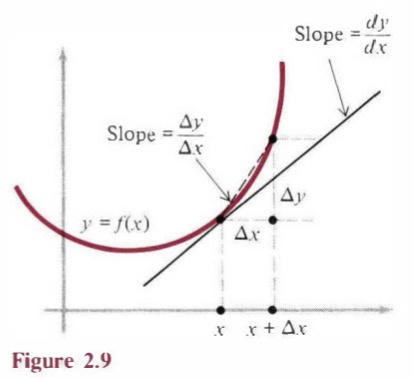
其中$\Delta y=f(x+\Delta x)-f(x)$，$\Delta y$ 不是$y$的一个任意变化量；而是x变为x+Δx时特定的变化量。我们知道，差商可以理解为y,x变化量之比，就是割线的斜率(图2)。莱布尼兹写出差商的极限形式，也就是导数f′(x)。用这个符号表示的话，导数的定义就变为

$$\begin{equation} \frac{dy}{dx}=\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \tag 2 \end{equation}$$

这就是图2中割线的斜率。$dy/dx$有两种不同的等价形式

$$\frac{df(x)}{dx}\qquad \frac{d}{dx}f(x)$$

对第二种形式，可以将$d / dx$看作一个运算，对函数$f(x)$运算得到它的导数$f′(x)$

$$\frac{d}{dx}f(x)=f'(x)$$

有一点非常重要，(2)中$dy/dx$是一个不可分割的符号。尽管书写形式上看可以，但是它不是平常意义上的两个变量$dy$与$dx$的商，因为他们没有定义，而且无法单独存在。在莱布尼兹的符号中，（2）中右边的极限形式象征性的用$\Delta$来代替字母$d$。从这个角度来说，导数的符号$dy/dx$提醒我们差商$\Delta y/\Delta x$以及$\Delta x\to 0$时计算极限的过程。从计算角度考虑也是有利的。当用莱布尼兹的符号时，许多基本的公式很容易被记住。
这个符号虽然好，但时也不完美。例如，加入我们要写出某个点的导数值，像$x=3$。因为$dy/dx$没有像$f′(x)$那样很方便的显示变量$x$，我们不得不用些难看的符号

$$\left( \frac{dy}{dx} \right )_{x=3}\qquad\left. \frac{dy}{dx}\right |_{x=3}$$

清晰明了的符号$f′(3)$明显比笨拙的表达时要占优势。
正如我们所看到的，上面的每种表达式各有各的优点。他们都广泛应用于科学和数学文献中，为了彻底熟悉他们，我们应该经常使用并且在他们之间自由的转换。

漫步微积分四——导数的定义