上篇文章中，我们学习了如何对和函数，差函数和常数乘函数进行求导。现在考虑

$$products\ uv\quad quotions\ \frac{u}{v}.$$

微分学有其自身的独特性和重要性，已被应用到物理、生物和社会科学中。它能够快速渗入到应用中，并得到问题的核心。然而，从整体效率的角度看，它的具体内容推迟一下，我们先花一点时间学习如何快速而准确的求导。

我们已经知道，对函数求导的过程称作微分。这个过程直接依赖于导数的极限定义，

$$f(x)=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$

或等价的

$$\frac{dy}{dx}=\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}$$

随着我们进一步深入主题，知道什么是连续函数就变得非常重要。在日常用语中，一个连续的过程表示处理中没有空隙或中断或突然的变化。大体说来，如果一个函数显示相似的行为那它就是连续的，也就是说，如果$x$发生小的变化，相应的$f(x)$值也发生小的变化。图1所示的函数在点$a$处是连续，因为$x$趋近$a$时，$f(x)$趋近$f(a)$。或更确切地说，$x$充分趋近$a$时，$f(x)$要多接近就多接近$f(a)$。用极限的语言说就是

$$\begin{equation} \lim_{x\to a}f(x)=f(a).\tag1 \end{equation}$$

目前为止，我们对于连续的陈述非常松散和直观，更像是在解释而不是定义。现在，我们将等式(1)作为函数$f(x)$在点$a$处连续的定义。我们发现，函数$f(x)$在点$a$处连续需要满足三个条件：$a$必须在$f(x)$定义域内，这样的话$f(a)$就存在；$f(x)$在$x$趋近$a$时有极限；这个极限值必须等于$f(a)$。我们通过图1可以更好的理解这些条件，函数在点$b,c,d$处不连续，并且不连续的方式也不同。在点$b$处，$\lim{x\to c}f(x)$存在但是$f(b)$不存在；点$c$，$f(c)$存在但$\lim{x\to c}f(x)$不存在；点$d$，$f(d),\lim_{x\to d}f(x)$都存在但值不相同。这个函数图存在三种不同情况的空隙或洞。

图1

前面给出的导数定义都依赖于函数极限的概念，我们对极限只做了最简短的解释。现在，我们已经知道了这一概念的目的，接下来关心一下它的意义。

考虑函数$f(x)$，自变量在点$a$的领域内都有定义，但是$a$ 点本身没定义。假设存在一个实数值$L$，当$x$越来越接近$a$时，$f(x)$越来越接近$L$(图1)。对于这种情况我们说$L$是$x$趋近$a$时$f(x)$的极限，用符号表示为

$$\begin{equation} \lim_{x\to a}f(x)=L.\tag1 \end{equation}$$ 图1

导数的概念与运动物体速度的计算密切相关。正是由于这一个事实，在牛顿努力寻找动力学定理并理解行星运动的思考中将微积分作为他基本的工具。看起来似乎只有物理系的学生有必要关注对于速度准确的想法。但是，这些想法对变化率这个广泛概念提供了非常简单的说明，这个概念在其他研究领域也非常重要，包括生物和社会科学。

在本节中，我们考虑速度问题的一个特殊情况:所讨论的对象可以看成沿着一条直行运动的点，所以它的位置由一个坐标(图1) 确定。如果我们知道每一时刻点的位置，那么真个运动轨迹就都已知，也就是说，如果我们知道位置$S$关于时间$t$的函数，

$$\begin{equation} s=f(t)\tag1 \end{equation}$$

为了方便，$t$的初始值通常从$0$开始。

图1

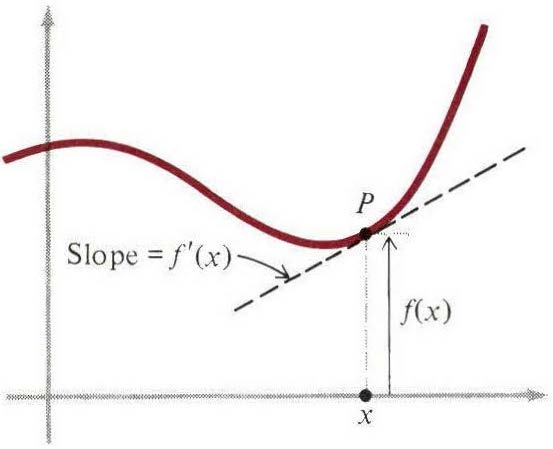
从几何上考虑，我们利用2.2，并丢掉下标$x_0$，就得到导数的基本定义：给定任意函数$f(x)$，导数$f′(x)$是新的函数，在点$x$处的值定义为

$$\begin{equation} f'(x)=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\tag1 \end{equation}$$

在计算它的极限时，$x$是固定的，而$\Delta x$是变化的且接近于零。某些$x$存在极限值，某些却不存在。如果$x=a$的极限值存在，就说函数在点$a$处可导。如果一个函数在其定义域内的每个点均可导，那么该函数是可导函数。这本书讨论的大部分函数都有此性质。
我们知道$f′(x)$可以像图1那样可视化，在图中$f(x)$是曲线上动点$P$的高度。然而，严格意义上讲，上述的导数定义不依赖于任何几何想法。图1构成一种几何解释，对理解导数来说非常重要，可以作为一种辅助手段，但它不是导数概念的基本组成部分。下一节我们将看到其他与几何无关的解释，那些解释跟几何解释同等重要。因此，我们必须将$f′(x)$作为纯粹的函数，并且需要认识到它有多种解释，但与其中任何之一都没有必要的联系。

各种想法都有自己的一席之地，但是时间会剔除许多细节。

$P＝(x_0,y_0)$ 是抛物线$y＝x_2$上的任意一个定点，如图2.4所示。作为基本思想的第一个图例，给定抛物线上一点P，计算切线的斜率。首先，我们选择曲线上的一个临近点 $Q=(x_1,y_1)$。接下来，我们画出由这两点确定的割线$PQ$，割线的斜率明显是：

$$m_{sec}={\rm slope\ of} \ PQ=\frac{y_1-y_0}{x_1-x_0}\tag 1$$

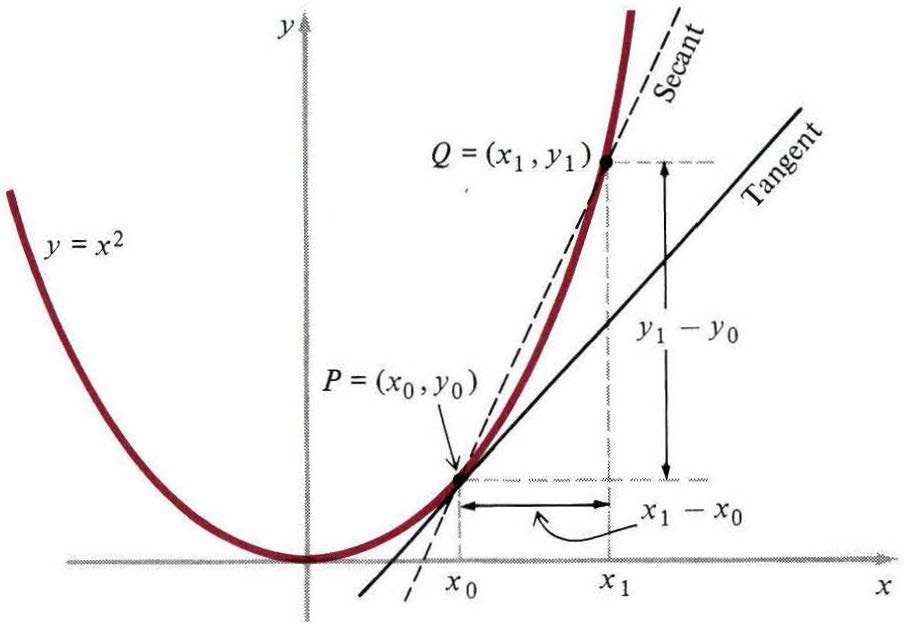
图一

大家都知道，我们生活的世界是以运动和变化为主导的。地球绕着太阳转动；向上扔一块石头，它的速度会慢慢变小停下，然后返回地面，并且速度一直增加；印度的人口每年增加，并且增长的速度也在增加；放射性元素的衰变。这些都是无数现象中的沧海一粟，而数学是沟通和理解他们最自然的媒介。伽利略在三百多年前就说过，“大自然最伟大的书籍都被写进了数学符号里”

我们以微积分是什么以及它为什么的重要来这两个主题开始我们微积分之旅。鸟瞰前方的道路可以让我们清晰的看到目的和把握方向，还将让我们更好的理解许多技术细节，而这些技术细节做成了我们微积分课程的大体内容。

    微积分通常分为两个部分，微分学和积分学。每部分都有各自的术语，繁多的符号和特定的计算方法。习惯这些需要大量的时间和练习，就像学习一门新语言一样。然而，这个事实不应把我们欺骗了，这门课核心问题真的很简单、很清晰，它们并不奇怪和神秘。

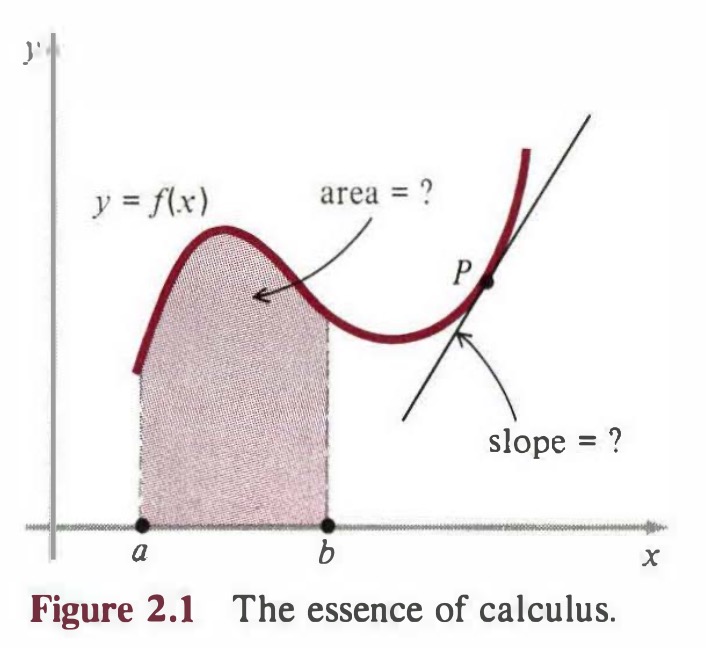
  几乎所有微积分解决的问题和想法，都围绕着两个非常容易理解的几何问题。它们都是关于函数 $y=f(x)$ 的图形。为避免复杂性，我们假设图像完全在x轴之上，如图2.1所示。

• 问题一 基础微分问题，切线问题：计算切线在函数图像给定点 $P$ 上的斜率
• 问题二 基础积分问题，面积问题：计算在$x=a$、$x=b$之间 函数图像下的面积
  

Appearances to the contrary, no writer deliberately sets out to produce an un­ readable book; we all do what we can and hope for the best. Naturally, I hope that my language will be clear and helpful to students, and in the end only they are qualified to judge. However, it would be a great advantage to all of us­ teachers and students alike-if student users of mathematics textbooks could somehow be given a few hints on the art of reading mathematics, which is a very different thing from reading novels or magazines or newspapers.

没有哪位作家会故意写没有可读性的书;我们也尽我们能做并抱以最好的希望。当然，我希望我的语言对于学生来说是清晰的，而最终也只有他们有资格来评判。但是，对所有教师和学生一样，如果学生的数学教科书在某种程度上给出一些读数学的方法，那将是非常有益的事。当然这与阅读小说或杂志或报纸并不是一回事。

In high school mathematics courses, most students are accustomed to tackling their homework problems first, out of impatience to have the whole burdensome task over and done with as soon as possible. These students read the explana­ tions in the text only as a last resort, if at all. This is a grotesque reversal of rea­ sonable procedure, and makes about as much sense as trying to put on one’s shoes before one’s socks. I suggest that students should read the text first, and when this has been thoroughly assimilated, then and only then turn to the home­ work problems. After all, the purpose of these problems is to nail down the ideas and methods described and illustrated in the text.

在高中数学课程中，大多数学生都习惯于首先处理家庭作业，对整体的课程任务没有耐心也希望尽快结束。这些学生只有在万不得已的时候才会阅读书上的解释。这真是完全颠倒的方法，相当于教一个人穿袜子之前先穿鞋。我建议学生首先阅读书本，当只是被彻底理解了，再转到作业上的问题。毕竟，这些问题的目的是为了确定书中描述与说明的想法与方法。

How should a student read the text in a book like this? Slowly and carefully, and in full awareness that a great many details have been deliberately omitted. If this book contained every detail of every discussion, it would be five times as long, which God forbid! There is a saying of Voltaire: “The secret of being a bore is to tell everything.” Every writer of a book of this kind tries to walk a nar­ row path between saying too much and saying too little.

学生想这样读书将会如何呢？慢慢地，会意识到许多细节被故意省略了。如果这本书写下讨论的所有细节，那么它会有现在的五倍之多。伏尔泰曾说:”无聊的秘诀在于告诉他一切”。每个作家试图在说得太多和太少选择折中的做法。

The words “clearly,” “it is easy to see,” and similar expressions are not in­ tended to be taken literally, and should never be interpreted by any student as a putdown on his or her abilities. These are code-phrases that have been used in mathematical writing for hundreds ofyears. Their purpose is to give a signal to the careful reader that in this particular place, the exposition is somewhat con­ densed, and perhaps a few details of calculations have been omitted. Any phrase like this amounts to a friendly hint to the student that it might be a good idea to read even more carefully and thoughtfully in order to fill in omissions in the ex­ position, or perhaps get out a piece of scratch paper to verify omitted details of calculations. Or better yet, make full use of the margins of this book to empha­ size points, raise questions, perform little computations, and correct misprints.

单词”很明显”“很容易看出”以及类似的表达式不应作就字面意思来理解，学生也不该理解为不需要去思考证明。这些是代码短语，曾出在数百年来的数学写作中。他们的目的是在那个特别的地方向细心的读者发出一个信号，（the exposition is somewhat condensed）计算的一些细节也许被省略。任何此类短语是对更细心学生的友好提示，或许需要拿出一张草稿纸验证省略的细节部分，或者可以充分利用这本书的空白地方，提出问题，简单计算一下或写出没有打印的部分。

George F. Simmons

CALCULUS WITH ANALYTIC GEOMETRY
漫步微积分一 —— 引言

下载redis dll库，更新php.ini

TP 3.2.3支持 PHP 7以上版本，没错找了半天发现是数据库配置不正确造成的。

架构-URL模式，用的兼容模式，譬如：
http://localhost/?s=/home/user/login/var/value

http://pecl.php.net/package/redis
Failed to initialize storage module:user
http://document.thinkphp.cn