泛函、变分和欧拉-拉格朗日方程

泛函

又被称为函数的函数，是将函数映射成数的方法。
传统的函数将数映射成数 $x -> f(x) -> y$;
泛函将 函数映射成数 $f(x) -> g(f) -> y$;

丢一些数进函数，得到一个数
丢一些方程进泛函，得到一个数

变分

用于分析一个泛函被扰动时的变化
相当于对一个泛函做微积分
变分法的关键定理是欧拉－拉格朗日方程。它对应于泛函的临界点。

变分的框架通常这样表示：

$$T = \int L(f(x), f(x)', x)dx$$

例如在最速降线问题中：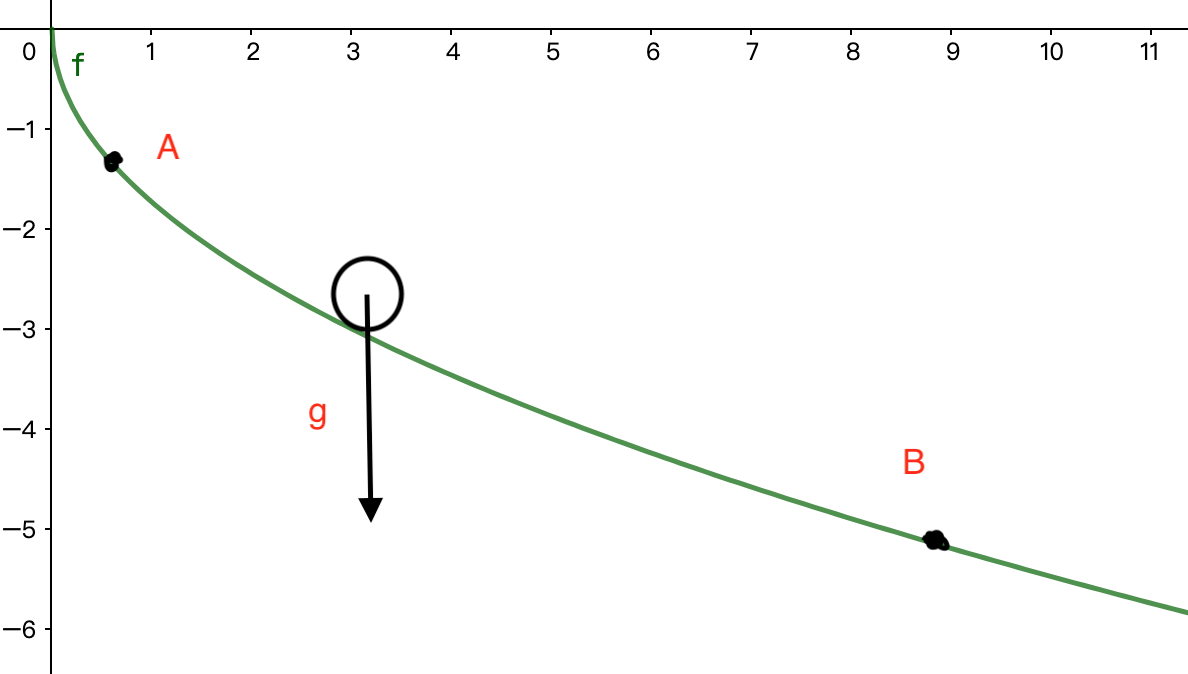

$f(x)$是小球的下落轨道
$f(x)’$是小球下落轨道的导数
$x$是小球的横向坐标
$T$代表从A落到B点所需时间

需要找到能使小球从A滚落B所需时间$T$最短的$f$

其中时间的表达式可以写成

$$\begin{array}{rcl} T &=& \int dt \\ &=& \int dL/V \\ &=& \int \frac{ \sqrt {dx^2+df^2})}{g\sqrt {\frac{2f}{g}}}dx \\ &=& \int \frac{ \sqrt {1+f^{'2}})}{\sqrt {2gf}}dx \end{array}$$

也就是距离微元除以当前速度的积分，将问题变为一个关于$f$, $f’$的积分问题。
在最速降线问题中仅涉及$f$, $f’$

E-L方程

欧拉-拉格朗日方程 用于求泛函极值

说明

在函数中，我们可以通过求函数导数等于零，求出局部极值。这意味着在该变量附近做微小的扰动，会出现函数值达不到极值的现象。

同样的，假设在泛函中的极值处，$f_0(x)$是最理想的解，如果对$f_0(x)$做微小的扰动$f_0(x)+\eta (x)$，会出现泛函数值达不到极值的现象。
表示为：

$$\int L(f_0(x) + \eta(x))dx \geqslant \int L(f_0(x))dx$$

构建

我们用 $\epsilon k(x)$ 来代替 $\eta (x)$，其中 $\epsilon$ 代表一个很小的标量，$k(x)$代表任意函数。
可以得到：

$$A(\epsilon) = \int L(f_0(x) + \epsilon k(x)) dx$$

将其转化为关于$\epsilon$的函数问题，我们需要证明：
在对于任意$k(x)$，导数$A(\epsilon)’ = 0$ 在 $\epsilon = 0$上取到。
其中扰动$k(x)$的两端同$f(x)$重叠不移动。
表示为：

$$A(\epsilon)' \vert_{\epsilon=0} \forall k(x)$$

这是经典的单值函数求极值问题

推导

$f_1(x) = f_0(x) + \epsilon k(x)$，用$f_1$来表示

由于是在这里积分求导是线性的，将其互换转入积分的内部:

$$A(\epsilon)' = \int \frac{dL(f_1(x), f_1(x)', x)}{d\epsilon} dx$$

根据积分链式求导，求关于$\epsilon$的偏导有：

$$\begin{array}{rcl} A(\epsilon)' &=& \int_{x_1}^{x_2} (\frac{\partial L}{\partial f_1} \frac{\partial f_1}{\partial \epsilon} + \frac{\partial L}{\partial f_1'} \frac{\partial f_1'}{\partial \epsilon}) dx \\ &=& \int_{x_1}^{x_2} (\frac{\partial L}{\partial f_1} k(x) + \frac{\partial L}{\partial f_1'} k(x)') dx \end{array}$$

根据积分分部求导 $(ab)’= ab’ + b’a$：

$$A(\epsilon)' = \int_{x_1}^{x_2} [\frac{\partial L}{\partial f_1} k(x) + (\frac{\partial L}{\partial f_1'}) k(x) \vert_{x_1}^{x_2} - (\frac{\partial L}{\partial f_1'})' k(x)] dx$$

由于在端点 $x_1$，$x_2$处，有约束所以$k(x_1) = k(x_2) = 0$：

$$A(\epsilon)' = \int_{x_1}^{x_2} [\frac{\partial L}{\partial f_1} - \frac{d}{dx} (\frac{\partial L}{\partial f_1'})] * k(x) dx = 0$$

可以得出E-L方程：

$$\frac{\partial L}{\partial f_1} - \frac{d}{dx} (\frac{\partial L}{\partial f_1'}) = 0$$

在满足该方程的条件下 $f_1(x)$ 是泛函极值函数
即：解函数相对于表达式的偏导 = 解函数导数相对于表达式的偏导变化率

引理

如果$F(f, f’, x) = F(f, f’)$ E-L 方程可以写成：

$$\frac{\partial L}{\partial f'}f' - L = C$$

$$\frac{d}{dx}(\frac{\partial L}{\partial f'}f') = \frac{d}{dx}(\frac{\partial L}{\partial f'}) + \frac{\partial L}{\partial f'}f''$$ $$\frac{d}{dx}(L) = \frac{\partial L}{\partial f} \partial f' + \frac{\partial L}{\partial f'} \partial f''$$ $$\frac {d}{dx}(\frac{\partial L}{\partial f'}f' - L) = f'[\frac{d}{dx} (\frac{\partial L}{\partial f'}) - \frac{\partial L}{\partial f}] = 0$$

可以看出方程的导数在极值处为零，方程等于常数。
即：解函数导数相对于表达式的偏导 * 解函数导数 - 表达式 = 常数

最速降线 与 第一次接触泛函
2.3．Euler-lagrange方程的推导