欧拉-拉格朗日方程练习

两点之间直线最短

写出AB两点间距离的变分表达：

$$L = \int_{x_1}^{x_2} \sqrt {1+f'^2}dx$$

写表达式的E-L方程：

$$\frac{d}{dx}(\frac{1}{2} \frac{2f'}{\sqrt {1+f'^2}}) = 0$$

化简后可得：

$$\frac{f'}{\sqrt {1+f'^2}}= C_1$$

可以得知解函数的导数是一个常数 $f’= C_2$
即AB间最短的距离是一条直线

求使旋转双曲面面积最小的函数

写出用盘圆法积分出面积的变分表达式：

$$S = \int 2 \pi x dl = \int 2 \pi \sqrt{1+f'^2} dx$$

写表达式的E-L方程：

$$\frac{d}{dx}(x \frac{1}{2} \frac{2f'}{\sqrt {1+f'^2}}) = 0$$

化简后可得：

$$\frac{xf'}{\sqrt {1+f'^2}}= a$$

继续化简可得：

$$f'= \pm \frac{a}{\sqrt{a^2-x}}$$

根据 $f’= \frac{1}{\sqrt{1-x^2}}$ 可得 $f = arc\cos(x)$
根据 $f’= \frac{1}{\sqrt{x^2-1}}$ 可得 $f = arc\cosh(x)$
重新规划 $x = x/a$ 可得 $f = a arc\cosh(\frac{x}{a}) + b$

线段能围出最大面积的形状是圆

需要用到泛函的拉格朗日乘子法：
有表达式$A_{min} = \int L(f, f’, x)dx$
在约束$B = \int G(f, f’, x)dx = Constant$下
构造 $C = (A - \lambda B)$ 求极值解

写出线段围出面积的变分表达式：

$$A = \int_{x_1}^{x_2} f dx$$

写出约束的变分表达式：

$$B = \int_{x_1}^{x_2} \sqrt{1+f'^2} dx$$ $$A - \lambda B = \int (f - \lambda \sqrt{1+f'^2}) dx$$

写表达式的E-L方程：

$$1=\frac{d}{dx} \frac{-\lambda f'}{\sqrt{a+f'^2}}$$

化简可得：

$$f' = \frac{a-x}{\sqrt{\lambda ^2 - (a-x)^2}}$$

即圆的微分方程，其中 $a-x$对应到 $\Delta x$， $\lambda$对应圆的半径。

最速降线问题

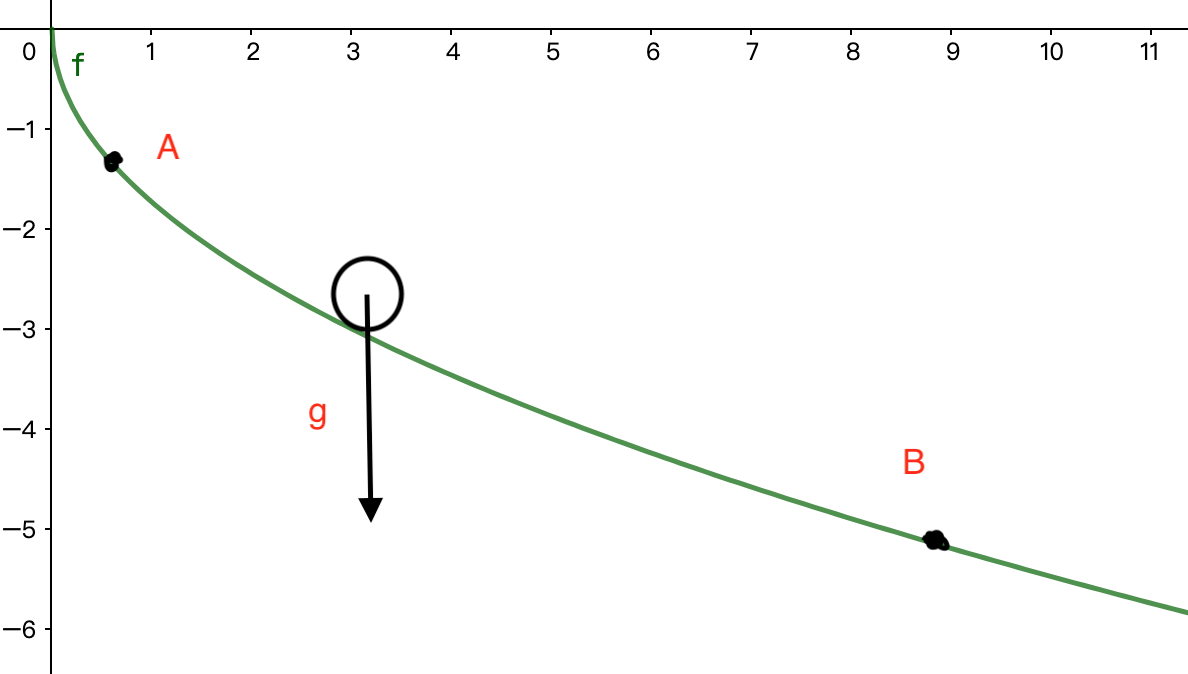
需要找到能使小球从A滚落B所需时间$T$最短的$f$

写出滚落所需时间的变分表达式：

$$T = \int \frac{ \sqrt {1+y^{'2}})}{\sqrt {2gy}}dx$$

用引理写出的E-L方程：

$$\frac{\partial T}{\partial y'}y' - T = \frac{1}{(1+y'^2)^{\frac{1}{2}}(2gy)^{\frac{1}{2}}} = C$$

化简后有$y(1+y’^2) = C’$

解：

上式是一个三角函数，设$x$是关于$x(\theta)$的函数，$y’ = \cot \theta = \frac{\cos \theta}{\sin \theta}$。
由于$y’$是关于x的微分，所以不能求出$y’$关于$\theta$的方程，把$y’$代入上式：

$$y(1+y'^2) = \frac{1}{\sin ^2 \theta } = C$$ $$y = C \sin ^2 \theta = \frac{C}{2} (1-2\cos 2\theta)$$

---

$x$的$\theta$表示

$$y' = dy/dx = \frac{dy}{d\theta} / \frac{dx}{d\theta}$$

转换成$x$关于$\theta$微元的表达式

$$\frac{dx}{d\theta} = \frac{dy}{d\theta}/ y' = \frac{C\sin 2\theta}{\cot \theta} = 2C \sin^2 \theta = C(1-\cos 2\theta)$$

$x$关于$\theta$的积分有：

$$\int dx = \int C(1-\cos 2\theta) d \theta$$

积分可得：

$$x + C_1 = C(\theta - \frac{1}{2} \sin 2\theta) + C_2$$

化简得：

$$x = \frac{C}{2}(2\theta - \sin 2\theta) + C_1$$

---

$y$的$x$、$y$表示

$\theta$角的变量表示

$$2 \theta = \frac{x - C_1 + 2a\sin \theta \cos \theta}{a}$$

用$a$来代替$\frac{C}{2}$，由于 $y = C \sin ^2 \theta$，有 $\sin \theta = \sqrt{\frac{y}{2a}}$、 $\cos \theta = \sqrt{\frac{2a-y}{2a}}$

$$2 \theta = \frac{x+\sqrt{y(2a-y)}}{a}$$

代回原式有：

$$\frac{y}{a} = 1 - \cos \frac{x+\sqrt{y(2a-y)}}{a}$$

2.4．Euler-lagrange方程的应用
3.1．拉格朗日乘子法
3.2. 泛函拉格朗日乘子法（一）
3.3. 泛函拉格朗日乘子法（二）
最速降线 与 第一次接触泛函